Abstract. Many modelling approaches can be used to assess evacuation time of buildings in fire situations. We present in this paper a new model, implemented in a collaborative work between LEMTA and CNPP, and based on a macroscopic continuous approach. First, the assumptions and algorithm of pedestrian movement model are detailed. Secondly, our model is confronted to results from full-scale tests carried out without any fire constraints and to other egress models on typical test cases extracted from literature. Finally, the complete model (including fire stresses) is compared with FDS+Evac on a simple fire scenario.
1. INTRODUCTION
Assessment of fire safety performance of buildings requires an estimation of Required Safe Egress Time (RSET) in fire situation. Many egress models have therefore been developed during the last decades, using various mechanisms. First evacuation models were based on empiric relations between people density, walking speed and geometric characteristics of the building (Togawa [1], Pauls [2]). Then, advancement of numerical simulation and progress in human behaviour modelling led to finer analysis of pedestrian motion, particularly microscopic approaches. For instance, Lagrangian-type models (Evac [3], Simulex) consider people as particles, whose respective motion is governed by different attractive or repulsive forces and characteristic velocities. Another kind of physical model, such as cellular automata (Blue and Adler [4], Klüpfel [5], Tissera [6]), considers a space-and-time discretization with people who jump from cell to neighboring cell following given transition laws. The main part of current evacuation computational tools are based on microscopic approaches. However, these kinds of models provide output results which are significant for the only simulated evacuation scenario and a particular initial people distribution. So, these microscopic descriptions need a statistical treatment of numerous simulations for a particular configuration to provide average data (required evacuation time, flowrates through openings in terms of persons per time unit) which can be considered representative of all scenarios likely to occur.
A macroscopic continuous egress model was developed in the present work, as an alternative to this limitation. Instead of considering people as individual entities with particular characteristics, our model tracks the evolution of people density in space and time and takes into consideration average input parameters to describe the population. The model is based on a people density balance solved in a discretized two-dimensional space, with additional constraints, such as critical flows through doors or congestion constraints, which make the problem more complex. The complete model is also able to take fire stresses into account, in terms of temperature, heat flux and visibility.
This paper details the algorithm used to solve the problem and our perspectives in order to integrate fire effects into the pedestrian motion model. Real-scale tests were carried out to check that our basis pedestrian motion model is able to reproduce experimental data (without any fire constraint). At this stage, validation of the complete model including fire stresses seems very difficult, due to the lack of experimental data. Nevertheless, a comparison between our model and FDS+Evac considering a simple test case extracted from literature leads to promising results.
2. THE EGRESS MODEL
The model presented here relies on a macroscopic approach, in which people are assembled to their people density. These types of models, based on partial differential equations solved in a continuous medium, have been studied since the 1950's with the emergence of first vehicular traffic models [7]. The application of these models inspired from fluid mechanics to people motion modelling is more recent and was initiated with Hughes [8]. In these studies, motion of people is described with the mass continuity equation, with some additional hypothesis in order to integrate human specificities and simple features of human behavior. Hughes' model was the source of further developments and mathematical studies. We can notice that macroscopic models are generally used in crowd motion with high densities. In fact, microscopic approaches are not optimal to study large crowds, due to the complex interactions between persons and the consequent computation time. This limitation is overcame with macroscopic approaches, in which calculation time depends on the size of computational domain instead of the number of persons. We can also notice that macroscopic egress models have been studied from a mathematical point of view, but have not been implemented in a numerical tool devoted to evacuation in fire situation.
2.1. Assumptions and formulation
2.1.1. Basis hypothesis
The people motion model follows the temporal and spatial evolution of a macroscopic quantity, which is the people density ρ (person per square meter). It is based on three fundamental assumptions:
- Without external constraint, people move at their preferred walking speed.
- People density has to respect a strict congestion constraint: it cannot exceed a critical density.
- Flowrate through a door cannot exceed a critical rate.
2.1.2. Mathematical formulation
Mathematically, a balance is written for the time- and space-varying people density in a pre-calculated velocity field:
where is the effective transport velocity of people density and is the preferred walking speed of people. The operator P refers to the projection of preferred speeds on the permissible velocity space in a least square sense. So, real speed is necessarily lower than preferred walking speed due to the presence of other persons.
2.1.3. Key parameters
To complete the evacuation model, we have to introduce four key parameters:
- Preferred or free walking speed , which depends on gender, age and culture.
- Reaction and premovement time , which is the time between the trigger of an alarm signal and the beginning of the evacuation. Evaluation of premovement time is particularly complex, because of its dependence on hazard perception. Nevertheless, its estimation is a crucial point in the sense that it can be longer than travel time towards exit.
- Critical people density , generally estimated between 4~6 persons per square meter. In this paper, the value of 5.4 persons per square meter is chosen.
- Critical flowrate through a door , which depends on the width of the opening. For a 90 centimeter-wide door, we can estimate it at 1,1 person per second.
2.2. Numerical algorithm without fire constraint
The implementation of our model and the algorithm used in order to solve it numerically (which is similar to the one adopted by Roudneff-Chupin [9]) are presented in figure 1. Two distinct parts are involved in a sequential process: subroutines PAULO (Pathfinding Algorithm Using Length Optimization) and MARCOE (Macroscopic Analysis of Rescue Configuration for Optimal Evacuation).
2.2.1. Scenario creation
The computational domain is discretized with a mesh of square cells, which can be classified into three categories:
- Walls and other impenetrable obstacles are considered as blocked cells which cannot be entered by people.
- Exit cells refer to the outward exit openings and are characterized by the critical flowrate.
- Free cells symbolize available space for motion and can be occupied by people.
The scenario (initial spatial distribution of persons) may be defined in a realistic way taking into account the nature of the building. Nevertheless, in order to study a mean configuration representative for all potential scenarios, the initial distribution of people density in the calculation area can be considered uniform and fairly distributed on free cells.
2.2.2. Preferred velocities computation
The preliminary step for the resolution of the density balance equation is the computation of the velocity field in which the people density is transported. This calculation is based on a simple observation: people tend to minimize their travel time to their goal [10]. So it is assumed in this study that people have a perfect knowledge of their environment and of the configuration of the building. For each free cell, the velocity is directed along the shortest path to the nearest exit cell. The shortest path between a current cell and its nearest exit cell is computed thanks to the PAULO algorithm (Pathfinding Algorithm Using Length Optimization) inspired from Dijkstra and able to take into consideration the specificities of the geometry (particularly blocked cells). At this stage, it can be noticed that the norm of the velocity is the preferred walking speed .
2.2.3. Transport at preferred speed
The space- and time-varying evolution of people density in the pre-calculated velocity field is governed by the equation (1). The equation is solved numerically using a finite volume method with an explicit temporal scheme. The advective part of the equation is treated thanks to a QUICK scheme, which consists in a second order interpolation in space and represents a good compromise between accuracy and computational time. At this step, exit cells are treated as particular cases and their outgoing flow is limited by the critical flux . Moreover, influence of surrounding people density on walking speed is not considered at this stage. This transport step is the first part of the MARCOE algorithm (Macroscopic Analysis of Rescue Configuration for Optimal Evacuation).
2.2.4. Corrective step
The previous calculation step (transport at preferred velocity) can lead to non-physical situations where the people density can locally exceed the critical density . So a corrective part extracted from literature [11] is introduced in order to respect congestion constraint for each cell. This corrective part consists in a stochastic projection of local excess density:
- The saturated cells are identified.
- For each saturated cell, the density excess is calculated and redistributed along a random walk, i.e. one of the four neighbors of the current cell is randomly chosen to receive as much density as it can to respect critical density.
- The random walk continues until the excess density is fully redistributed.
It should be noticed that this corrective part is mathematically equivalent to Equation (2) and consists in its algorithmic implementation. This step is the second part of the MARCOE algorithm.
2.3. Integration of fire effects
The present model allows the inclusion of fire influence on egress conditions.
Fire effects on humans are generally classified into three categories:
- Thermal effects in terms of temperature and heat flux: high temperatures can generate hyperthermia (increase in body temperature with alteration of mental abilities) and respiratory tract burns. Heat flux (from fire source and smoke layer) is responsible for skin burns.
- Optical effects: gases and soot particles present in smoke can reduce strongly the visibility distances due to their extinguishing properties. This loss of visibility may have a significant impact on evacuation process, because it is one of the most influent criteria on decision-making.
- Toxic effects: three different toxic effects are identified in literature. Asphyxiating gases affect the transportation of oxygen in the human system; irritant gases inflame human tissues and cause pains. Narcotic gases affect physical capabilities and can lead to loss of consciousness.
In this study, it was decided not to deal with the question of toxic effects, because we can consider that toxic effects are correlated with optical and thermal effects. Moreover, reliability of gas concentration estimation sub-models (especially those embedded in Fire Dynamics Simulator) is questionable.
Three different ways are considered to represent fire impact on evacuation circumstances:
-
Burning cells are treated as blocked cells (physical obstacles)
-
The cells with thermal constraints (temperature, heat flux) and optical constraints (optical density) above threshold values introduced in table 1 are also considered as blocked cells. In fact, beyond these threshold values, it can be generally considered that people are not able to ensure their own evacuation. The critical value chosen for extinction coefficient corresponds to a visibility distance of 10 m according to Jin's correlation for a light-reflecting object.
-
Extinction coefficient of the smoke locally reduces the walking speed of humans according to the empirical formula given by Frantzich and Nilsson [12]:
(3)where is the effective speed, is the preferred speed and is the extinction coefficient (). Fire-related data are extracted from Fire Dynamics Simulator 6 (developed by the NIST) and are updated at each time step.
| Fire effect | Threshold value |
|---|---|
| Temperature | 60°C |
| Thermal flux | 2,5 |
| Extinction coefficient | 0,3 |
3. VALIDATION AND COMPARISON BETWEEN MODELS
3.1. Validation without fire stresses
To the authors' knowledge, macroscopic models based on people density conservation have not been validated rightfully against real data yet. The objective in this section is to validate the evacuation model at a small scale with repeated tests and without fire constraints.
3.1.1. Experimental setup
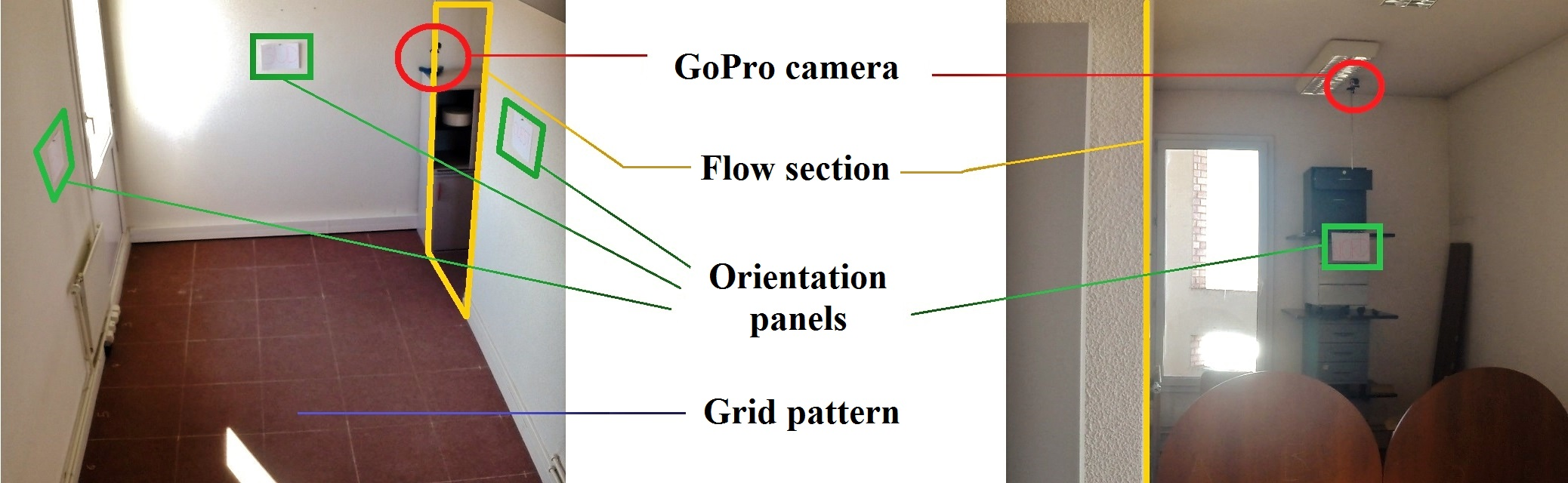
The egress model was confronted against experience on a very simple configuration: a 10 m² room (4 m long and 2,5 m wide) with a single 90 centimeter-wide exit (figures 2 and 3). A GoPro camera is set at the door in order to take the evacuation time of each person and to determine at every moment the proportion of initial population which is out of the room. Initial positions and orientations of the 10 persons are randomly chosen and the start for evacuation is given by a sound signal.
3.1.2. First step: identification of walking speed and reaction time
The aim of this preliminary step is to determine, for this particular experimental configuration, the average free walking speed and reaction time of the 10 members of the population. 100 evacuation tests were carried out with a single person to obtain exit rate (percentage of the population who left the room) over time (figure 4).
The analytical expression of this exit rate allowed the identification in a least square sense ((4),(5)) of mean preferred walking speed V0 and mean reaction time of the population:
In this particular case, the identified reaction time includes the reaction to a beep and the orientation towards the exit. It can be noticed that average free walking speed of our sample is particularly low due to the compact dimensions of the room.
3.1.3. Validation with 10 persons
20 repeated egress tests were conducted with the same sample of 10 persons to obtain average data significant for many different scenarios. Walking speed and reaction time identified in the previous step were introduced into the code as input parameters. Figure 5 represents mean experimental values (red), the solution computed by our code which takes congestion constraint into consideration (green), and the analytical solution which considers that people evacuate the room as if they were alone (blue).
These results provide two main insights:
- Congestion is correctly taken into account.
- Evacuation rates computed from a unique simulation with a mean scenario are similar to those obtained by a statistical treatment of 20 particular random scenarios.
3.2. Comparison with other codes
In this paragraph, we compare output results from our model with those obtained with other evacuation codes. The chosen scenario for this comparison is the one described in Test 9 extracted from the Guidelines for evacuation analysis for new and existing passenger ships, of International Maritime Organization [13]. Characteristics of the test case are presented in Table 2.
| MARCOE PAULO | Other codes | |
|---|---|---|
| Number of persons | 1000 | 1000 |
| Initial spatial distribution | uniform | random |
| Free walking speed | 1.295 | uniform distribution between 0.97 and 1.62 |
| Reaction time | 0 s | 0 s |
| Critical flowrate | 1.1 | undefined |
| Critical density | 5.4 | undefined |
| Number of simulations | 1 | variable |
Table 3 presents the evacuation times computed with different numeric tools.
| Code/model | Evacuation time (s) |
|---|---|
| Evac [3] | 240.8 |
| Pathfinder (Steering mode) [14] | 196.7 - 199 |
| Pathfinder (SFPE mode) [14] | 264.7 - 275.6 |
| Pathfinder (Steering+SFPE mode) [14] | 273.2 - 283.2 |
| Zhang's model [15] | 251 - 252 |
| PedGo 2.5.0.7 | 179 |
| MARCOE PAULO | 228 |
The evacuation time computed with our model MARCOE PAULO is coherent with output results of other codes. Nevertheless, it can be noticed that egress times calculated with different models are included in a very wide range of values. The lack of details on input parameters used in the different codes makes interpretation of these deviations particularly difficult.
4. INTEGRATION OF FIRE EFFECTS: COMPARISON WITH FDS+EVAC
4.1. Comparison case
The geometry of our study case is the one adopted in Test 10 extracted from the Guidelines of IMO [13] (figure 6). It consists in a group of open boat cabins with two exits. One of the cabins contains a fire source whose nominal heat release rate is 1 MW. It is assumed that the heat release rate is governed by a medium growth according to NFPA 204 standard. Fire-related data (extinction coefficient, temperature, thermal flux) are extracted from FDS at 1.8 meter high and are updated every 5 seconds. A population of 23 persons is considered with uniform characteristics (preferred walking speed of 1.25 and reaction/pre-movement time of 30 s).
4.2. Numerical results
Evacuation process is simulated with our macroscopic model, and exit rate over time is compared with the one obtained by a statistical post-processing of 30 simulations conducted with FDS6+Evac (figure 6).
Table 4 presents intermediate evacuation times calculated with both codes ( is the time that n % of the initial population is outside).
| EVAC | MARCOE PAULO | |
|---|---|---|
| 40.1 s | 38.4 s | |
| 43.2 s | 41.0 s | |
| 45.7 s | 43.1 s | |
| 47.2 s | 44.1 s | |
These numerical results show that evacuation rates over time have a similar evolution for both models, and that a maximal flow rate through doors is observed when congestion appears close to exits. Discrepancies can be explained by considering the different assumptions made by the models, especially the decision making sub-models embedded into FDS 6+Evac.
5. CONCLUSION
An evacuation model based on a macroscopic continuous approach has been developed in order to provide reliable estimations of evacuation data (egress times, flow rates) for a particular building configuration. To overcome potential limitations of discrete models in terms of computational time, it consists in the tracking of people density over time in a 2D domain. Evolution of people density is governed by a balance equation and additional constraints treated by a specific algorithm to include interactions between walking speed, density, congestion formation and people flows. First validation tests performed at a small scale seem promising and prove that our model is able to handle congestion properly. Comparison tests with other egress codes (and particularly the one embedded in FDS 6) on simple scenarios revealed that the model gives similar output data than usual models used in Fire Safety Engineering. They also showed that a unique simulation with our model can provide significant egress times and avoid heavy computations of numerous particular scenarios. Complementary developments are still ongoing to improve the reliability of the model. One of our main perspectives is the improvement of the inclusion of fire effects in the pedestrian model. The current method consists in considering threshold values to assess tenability of egress conditions. In fact, fire effluents have a more complex influence and may have a strong impact on evacuation below a critical value. This further development will make our model more realistic, and more robust from a numerical point of view.